Recursividade em Java

A recursividade é uma técnica de programação onde uma função chama a si mesma para resolver um problema maior, dividindo-o em subproblemas menores. Em Java, esse conceito é amplamente utilizado para resolver problemas que possuem uma estrutura repetitiva ou hierárquica, como cálculos matemáticos, manipulação de estruturas de dados como árvores, e muito mais.

Estrutura de uma função recursiva

Para que uma função recursiva funcione corretamente, ela precisa seguir duas regras principais:

1. Caso base: Uma condição que termina a recursão e impede que a função continue chamando a si mesma indefinidamente;
   
   
2. Passo recursivo: A parte da função onde ela faz a chamada a si mesma, quebrando o problema em subproblemas menores.

Abaixo está um exemplo simples de uma função recursiva que calcula o fatorial de um número:

public class Fatorial {
    public static int fatorial(int n) {
        // Caso base: fatorial de 0 ou 1 é 1
        if (n == 0 || n == 1) {
            return 1;
        }
        // Passo recursivo: n * fatorial de (n - 1)
        return n * fatorial(n - 1);
    }

    public static void main(String[] args) {
        int numero = 5;
        int resultado = fatorial(numero);
        System.out.println("Fatorial de " + numero + " é: " + resultado);
    }
}

Explicação:

• Quando chamamos fatorial(5), a função se chama recursivamente até que o valor chegue a 1, que é o caso base;
  
  
• O fatorial de 5 é calculado como 5 * fatorial(4), que continua até 1 * fatorial(0). Quando o caso base é alcançado, a função começa a retornar os valores.

Recursividade e pilha de chamadas

Quando uma função recursiva é chamada, as chamadas são empilhadas na pilha de chamadas (call stack). Cada chamada recursiva empilha uma nova instância da função até que o caso base seja atingido. Quando isso acontece, as funções começam a ser desempilhadas, e os resultados começam a ser retornados para as chamadas anteriores.

No exemplo do cálculo do fatorial de 5, a pilha de chamadas funcionaria assim:

fatorial(5)
fatorial(4)
fatorial(3)
fatorial(2)
fatorial(1) -> caso base

Uma vez que o caso base é atingido, a pilha começa a ser esvaziada:

fatorial(1) retorna 1
fatorial(2) retorna 2 * 1 = 2
fatorial(3) retorna 3 * 2 = 6
fatorial(4) retorna 4 * 6 = 24
fatorial(5) retorna 5 * 24 = 120

Recursividade em problemas comuns

A recursividade é frequentemente usada para resolver uma série de problemas clássicos. Vamos ver dois exemplos populares: a sequência de Fibonacci e a travessia de árvores.

Sequência de Fibonacci

A sequência de Fibonacci é uma série de números onde cada número é a soma dos dois anteriores. Usar recursividade para calcular Fibonacci é simples:

public class Fibonacci {
    public static int fibonacci(int n) {
        if (n <= 1) {
            return n;
        }
        return fibonacci(n - 1) + fibonacci(n - 2);
    }

    public static void main(String[] args) {
        int numero = 6;
        int resultado = fibonacci(numero);
        System.out.println("Fibonacci de " + numero + " é: " + resultado);
    }
}

Travessia de Árvores

Árvores binárias são outra estrutura onde a recursividade é frequentemente utilizada para percorrer os nós. Aqui está um exemplo de travessia in-order (esquerda, raiz, direita) de uma árvore binária:

class No {
    int valor;
    No esquerda, direita;

    public No(int item) {
        valor = item;
        esquerda = direita = null;
    }
}

public class ArvoreBinaria {
    No raiz;

    // Função recursiva para travessia in-order
    void inOrder(No no) {
        if (no == null) {
            return;
        }
        inOrder(no.esquerda); // Percorre a subárvore esquerda
        System.out.print(no.valor + " "); // Visita o nó atual
        inOrder(no.direita); // Percorre a subárvore direita
    }

    public static void main(String[] args) {
        ArvoreBinaria arvore = new ArvoreBinaria();
        arvore.raiz = new No(1);
        arvore.raiz.esquerda = new No(2);
        arvore.raiz.direita = new No(3);
        arvore.raiz.esquerda.esquerda = new No(4);
        arvore.raiz.esquerda.direita = new No(5);

        System.out.println("Travessia in-order da árvore binária:");
        arvore.inOrder(arvore.raiz); // Output: 4 2 5 1 3
    }
}

Vantagens e desvantagens da recursividade

Vantagens:

• Simplicidade e legibilidade: Problemas que são naturalmente recursivos, como a travessia de árvores, podem ser resolvidos de forma mais direta;
  
  
• Divisão de problemas complexos: Funções recursivas quebram problemas maiores em partes menores e mais gerenciáveis.

Desvantagens:

• Uso de memória: Cada chamada recursiva ocupa um espaço na pilha de chamadas, o que pode levar a um estouro de pilha (stack overflow) se a profundidade de recursão for muito grande;
  
  
• Desempenho: Em alguns casos, como na sequência de Fibonacci, a recursividade pode ser menos eficiente que outras abordagens iterativas, pois há muitas chamadas repetitivas.

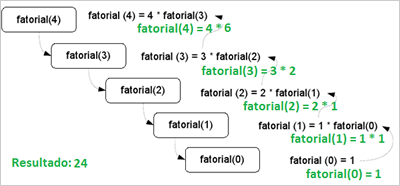
Outro exemplo prático

Abaixo temos um esquema que ilustra o conceito de recursão e um exemplo de codificação que é frequentemente usado para explicar a recursividade:

public int soma(int n) {

   //a soma de n com 0 é o próprio n 
   if(n == 0) {
		
	return n;
   }
	 return  n + soma(n - 1);
}	
    
//Se n = 4, então soma(4): 
     
/* return 4 + (4-1) = 7
   return 7 + soma(3-1) = 9
   return 9 + soma(2-1) = 10     
*/ 
        
public int fatorial(int n) {
	
   if(n == 0) { //fatorial de 0 é 1     
	return 1;  
 
	//senão...      
	return  n * fatorial(n - 1); 
   }  
    
//Se n = 4, então fatorial(4):
    
/* return 4 * (4-1) = 12
   return 12 * fatorial(3-1) = 24
   return 24 * fatorial(2-1) = 24     
*/ 

A recursividade é uma técnica poderosa para resolver problemas complexos de maneira mais intuitiva e elegante.

No entanto, é importante compreender suas limitações, especialmente em termos de eficiência e uso de memória. Ao dominar a recursividade, você estará equipado para enfrentar uma ampla gama de desafios de programação em Java.

Dúvidas ou sugestões sobre recursividade em Java? Deixem nos comentários! Para mais dicas, acesse o nosso canal no YouTube:
https://youtube.com/criandobits

Tags: recursividade